Why was this bullet visible?

Tell me about your camera position. It looks like the camera is square to the target, but below it in elevation, as the target looks square without any apparent distortion and I am assuming your target is square to your shooting position. The bullet appears to fall to the target from the 1 o’clock position. Is there a crosswind, great group if so, or is the camera set left of bullet path? Perhaps there was a flaw in the bullet that caused it to be less stable causing it to be more visible and creating a flyer. ~
~1f~Now you must be closely examining all your footage especially the flyers. Flyers are the bane of target shooters.
I was spotting for a shooter in Connaught when the butts called back with 9/10 hits. Every one I watched had the usual movement of earth behind the target and the bullet swirl looked good on all. Butts officers do not believe that two bullets can pass through the same hole but it has to happen sometime.
 
I shot about 70 rounds Sunday and out of those 70 I only seen 1 bullet drop in and guess what it went exactly where I aimed. I'm calling a coincidence.
 
grauhanen said:
To conclude the matter, let's call it coincidence.

Maybe there should be a rule that says when three or four previous posters say the same thing, it must be true.;)
Click to expand...

Maybe there should be a rule that says when the OP doesn't find someone that agrees with them then everyone else must be wrong.
 
I hope nobody takes my previous post too seriously, I couldn't resist playing devil's advocate.

Let's try to explain this with some math/logic. So, at 100 yards the bullet is traveling in the neighborhood of 930 feet per second. I have to make an assumption, let's say your camera was 9.30 feet away from the target. In that case the bullet would spend 0.01s (1/100s) within the view of the camera. Assuming your camera is recording at 60 frames/second, that's one frame every 0.01667 seconds. The bullet would, on average, be in and out of the view of the camera between frames. There will be some instances where the bullet is captured.

This is, for all intents and purposes, random. I'm going to make one more assumption - this is what most people have been referring to as the coincidence.
 
People shoot Eley so you can see it, I won't call it 'trace' I'll call it 'reflection off the back of the bullet' (especially away from the sun) Also why I don't line up to shoot early at our range with everyone else, shooting straight East, I prefer having better light on the target and splash area around the gongs out at 300m when its windy. It gives me better feedback.
 
sk8snwmx said:
People shoot Eley so you can see it, I won't call it 'trace' I'll call it 'reflection off the back of the bullet' (especially away from the sun) Also why I don't line up to shoot early at our range with everyone else, shooting straight East, I prefer having better light on the target and splash area around the gongs out at 300m when its windy. It gives me better feedback.
Click to expand...

It's more likely that shooters who use Eley do so because of how it performs on target rather than because they wish to see it in flight. It also often leaves a very clear hole in most target papers, perhaps a product of the EPS bullet shape.
 
Id tend to agree with Emerson. Coincidence is not a thing but an excuse for not finding the cause. I’ve never heard of shooting a certain brand of ammo so the bullet can be seen. If your shooting from a solid position and with proper form, many rounds should be visible with quality optics when using rimfire match ammo. While spotting at matches this happens regularly. The weather conditions play an important role for sure! It would be interesting to see high speed photography of 100 rounds and track their poi compared to the film of their flight characteristics. Interesting things about rimfires
 
At 50m, using my Sightron 45 x 45 (ED glass), I see the last moments of the bullet's flight of most of the crazy fliers that hit outside lateral or very low, diverging away from the perpendicular line of the point of aim (POA), between and below about 9 o'clock and 3 o'clock. The crazy fliers that hit very high above POA (above 3 o'clock and 9 o'clock), I usually cannot see the bullets. The most consistently visible bullets are the crazy flier rounds that drop really low to the 6 o'clock area well below POA.

At 50m, I usually can never see the bullets through the scope that hit the 10 and X rings, which is most in-line to my POA (central axis of the lens). The bullet is arcing down at impact, but the field of view through the 45x scope is small, so the peak of that arc may be outside the field of view.

In that small field of view, the perfect shot is only being seen from the back of the bullet. But the flier is being seen slightly from the side of the bullet as well, because the POA is in the center of the glass....., except for the bullets that drop into the 6 o'clock POI, which I cannot explain for how easy those are to see. Those 6 o'clock drops are on almost the same downward arc as the perfect POI's, so they should be difficult to see, but instead they are easy to see.

Anecdotally, my eyes are seeing the same sort of trend what Grauhanen is reporting with his camera evidence: There is something about many of the crazy fliers that veer way off from POA that makes them more visible....and I state this as a hypothesis, not a truth or proof. I have no experimental evidence.

I have thought about this for years. Some of my hypotheses/thoughts are (and this is just dumb brainstorming):

1) We know that all lenses (because they are curved) distort light to some degree, except for the precise center of the lenses (optical axis). Your eye for your POA should be in the precise center of the glass to minimize parallax. As the path of the bullet moves away from the POA and away from the lens center, its reflected light is more distorted than when it is closer to the center of the lens. Perhaps this distortion makes the bullet more visible?

The flight of the perfect center-X hits are of course an arced flight, and only hit at the POA at the last moment of flight. The perfect hits also have their entire flight arc that is outside the high mag lens's central axis and POA until the precise moment of impact. Therefore this distortion and parallax hypothesis does not explain everything (anything) cleanly, and may be critically flawed.

But, the perfect shot is flying into the center of the lens where distortion is less. The crazy flier is flying away from the center of the lens into a zone of more lens distortion.


2) If the crazy flier issue is a bad bullet (e.g., a center of gravity/shape flaw), then the bullet likely has significant wobble (pitch and yaw). This motion will create more turbulence in the wake, causing more light refraction and therefore light distortion (i.e. more mirage effect in the bullet trace). Its that extra distortion your eye/camera may be seeing, added to the parallax effect of the flier.


At 100m with my 45x power scope, I see many more last moments of bullet flight, both perfect hits and fliers. At 100m, therefore I think this is a different visual phenomenon for eye or camera sensor because (a) more flight time, and the bullet is slowing down to fewer frames per second, and (b) where more or all of the bullet's arc is within the field of view, and there is simply more time to see the bullet and its trace. Trace visibility, depending on temperature, dewpoint, humidity, and light angle, is quite variable.

At 100m with my 3-9x power hunting scope, I can see most subsonic rimfire bullets (perfect shots and fliers), if the light and atmospherics are good. The field of view is the entire arc of flight, and well within the human eye's capability to see objects in motion. At this distance with the low power scope, fliers are no different for visibility to my eye than perfect hits.

In my experience, as the glass magnification increases and field of view decreases, the visibility of bullet in flight for my eye decreases to mostly only the fliers being visible.

Grauhanen: A potential experiment for your camera is to zoom out, step-wise to lesser zoom magnifications, to allow a larger field of view, which will provide more in-flight time for the camera sensors to record bullet flight. If you were to find a zoom magnification for your camera where many bullets started to be "seen" by the camera, both fliers and good hits, you may be able calculate if its a random effect, or indeed an effect for fliers that are more visible.

It is a tough experimental design, because fliers by defintion are rare in good target ammo (maybe 1 or 2 per box of 50 rounds?), and so sample size will have to be large to prove experimentally if fliers were more visible.
 
With a target at 50 m the bullet never even breeches 0.5" above the boreline. A 1085 fps shot has about a 0.41" peak. You should be able to see its entire flight once it comes into view from underneath the scope without much trouble. The field of view isn't that small. I have no trouble watching them during benchrest shoots through my Sightron set at 50x, and can see a substantial amount of the target at that magnification. Even with a target at 100 m the peak only grows to 3.69", which you should still have no trouble seeing in the scope the whole time. Even when I'm shooting silhouette with the 32x scope on that gun I can often watch bullets the whole way out to the target, though this varies more since I'm standing and wobbling around as a result. :D

As for bad bullets, well, the data I showed earlier says that even a random lot of Tenex might have a ~5-10% rate of unusual bullets depending on your rejection tolerance. I looked at a few more today with a 1.64x SD rejection tolerance. The actual BC numbers are garbage because I haven't input any atmospheric data, so it is just using the defaults, and so no point in listing them. The important part(s) to look at are how many shots got rejected, and maybe what the SD is. Anything with a difference greater than 1.64x SD got rejected.

uc


As you can see, none of them are immune to having bullet differences. Most of the sample sizes here were 100, but a few were only 25, like the CCI Pistol Match with only 1/25 rejected, and the CCI Clean 22 with only 2/25. I didn't have sample sizes of 100 for all of them, but including the smaller sample sizes was still of some interest. The main point being, they've all got a certain amount of bullets that differ from the average bullet, and those are all going to do something slightly different in the air.
 
_Shorty said:
With a target at 50 m the bullet never even breeches 0.5" above the boreline. A 1085 fps shot has about a 0.41" peak. You should be able to see its entire .
Click to expand...

Not that it makes a difference, but a 1085 fps .22LR round zeroed at 50 has about 1" peak height over the bore line. (At 100 yards, it's about 4.35".)

 
My mistake, JBM takes into account scope height over the bore, which I tend to forget about for some reason, and with that removed from the equation it is indeed 1" at its peak. Thanks.
 
I am confused guys regarding "bore line", and field of view.

Bore line:

The bullet never travels over the bore line (axis drawn to infinity for the pointing direction of the bore).

The bullet drops downwards forever from the bore line the instant it leaves the muzzle, never crosses it, and creates an arc falling below the bore line's axis until it hits the target, (hopefully at its zero'd height), which is in direct line with the optic's line of sight. I know you guys know all this, I am just trying to clarify my understanding of the terms being used.

Did you mean the bullet's rise above the optic's line of sight? As you mentioned, this number will depend on how high the optic is mounted from the barrel's bore axis.

Absolute drop is the bullet's total drop due to gravity from the muzzle. Its a continuous increasing negative number downwards, negative from the muzzle axis. That same drop when calculated for the trajectory relative to the line of sight, is the same arc tilted upwards (as per the bore axis angle), which begins negative below line of sight, crosses line of sight, becomes positive above it, then drops to line of sight zero at the zero'd range.

Sketch below, (not to scale), for a high magnification BR scope (45 to 50x), which sees a few inches of target height at 50m, showing:

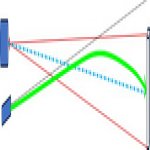
Line_of_Sight_Bullets_Path_resized.jpg

- black dashed line is the bore axis direction

- blue dot-dashed line is the line of sight from the center of the scope

- Red lines show the focused outer light beams reflecting off the target, focused into the center of the optic.

- Solid green line shows the bullet's trajectory, dropping continuously from the bore axis. But it rises above the line of sight, then drops to its zero'd point on target


Field of View:

In this high magnification scope example, the bullet starts below and outside the cone of light focused from the target. Therefore the bullet or trace cannot be visible for the first part of its flight.

I ran a quick scenario in JBM using a JBM library Lapua bullet, zero'd at 50m, 1.5 inch scope mount, MV 1085. It crossed elevation 0, i.e. the line of sight, at 15m from the muzzle. Due to the entry angle of the focused beam, it comes into the edge of the beam earlier than 15m, but its likely going to be impossible for the human eye to pick up at that entry point. The bullet needs time in flight inside the focused beam to generate enough movement image for your eye to pick it up. Roughly the first third of the bullet's flight is going to be invisible in this scenario because its below the focused line of sight cone

The lower the scope is mounted, the sooner the bullet can become visible for a given magnification.

As the scope power decreases, the field of view for where that bullet enters the focused beam should move towards the shooter, (again influenced by scope height), allowing more time for your eye to pick up the flight image. At a scenario of low scope magnification, almost the entire flight will be inside the line of sight focus beam due to the angles of focus into the center of the scope, e.g. a 9x magnification at 100m you can see almost the entire flight.

EDIT: There is a mistake in the sketch. See addendum edit post #37
 

Attachments

  • Line_of_Sight_Bullets_Path_resized.jpg
    Line_of_Sight_Bullets_Path_resized.jpg
    23.1 KB · Views: 61
Last edited:
_Shorty said:
Draw a line between the muzzle and the target and call that whatever you like. ;) Bullet goes over that every time unless you aim down.
Click to expand...

No.

Gravity is relentless. The bullet accelerates downwards immediately from the muzzle at 9.8m/s/s. The bullet never crosses (goes over) the axis of bore.
You can aim upwards or downwards, the bullet falls downwards to the Earth away from the axis of the bore.

The only time the bullet would track precisely on the bore axis, would be with the bore shooting perfectly straight up or straight down (at right angle to the center of the Earth), but it would never cross that path (unless there was wind of course, and technically because of air density, it likely would because of slight spindrift force).

The bullet crosses the axis of aim from the scope, aperture or iron sights at sufficient distance, and that trajectory crossing over the line of sight depends on the zero'd distance (and bullet's ballistic variables for velocity, drag, etc).

Shooting a target well inside the zero'd distance, at a short distance, will mean the bullet does not cross the line of sight either. e.g. Real life, I zero my grouse rifle at 20 m (subsonic hunting hollowpoint), with scope center at 1.5" above the bore. At 10m, the bullet never crosses the line of sight and hits about 3/4 to an inch low, below the line of sight. Bullet is still rising to cross the line of sight at or just before 20m. Therefore at 10m, I hold crosshair on the grouse top of head, and the bullet will hit below at center of head or top of neck (or will miss because I am shaky with offhand shooting, but that's another story :) ).
 
EDIT: I made a mistake in the sketch above in post #34.

The focus point of the light beams back from the target do not have to be focused just at the front of the scope's lens, although some can be and that will be focused in the glass. The light rays can be spread wider to an extent towards the outside of the lens, and the glass lenses will focus the beam for the eye. The width and angle variation of that light beam spread that can be focused, is dependent on the optical quality, especially its depth of field properties.

So in my sketch, that cone of visibility would extend a little more towards the shooter.
 
Biologist said:
No.

Gravity is relentless. The bullet accelerates downwards immediately from the muzzle at 9.8m/s/s. The bullet never crosses (goes over) the axis of bore.
You can aim upwards or downwards, the bullet falls downwards to the Earth away from the axis of the bore.

The only time the bullet would track precisely on the bore axis, would be with the bore shooting perfectly straight up or straight down (at right angle to the center of the Earth), but it would never cross that path (unless there was wind of course, and technically because of air density, it likely would because of slight spindrift force).

The bullet crosses the axis of aim from the scope, aperture or iron sights at sufficient distance, and that trajectory crossing over the line of sight depends on the zero'd distance (and bullet's ballistic variables for velocity, drag, etc).

Shooting a target well inside the zero'd distance, at a short distance, will mean the bullet does not cross the line of sight either. e.g. Real life, I zero my grouse rifle at 20 m (subsonic hunting hollowpoint), with scope center at 1.5" above the bore. At 10m, the bullet never crosses the line of sight and hits about 3/4 to an inch low, below the line of sight. Bullet is still rising to cross the line of sight at or just before 20m. Therefore at 10m, I hold crosshair on the grouse top of head, and the bullet will hit below at center of head or top of neck (or will miss because I am shaky with offhand shooting, but that's another story :) ).
Click to expand...

Uh, yes. Pretend the red line below is a straight line from the muzzle to the target. Dotted line is arc the bullet follows since you've lobbed it at an upward angle. Unless your target is way downhill your bullets ALWAYS go above the red line because you're angling your barrel upwards. I know what you're saying. But that's not what we're talking about. The red line in my museum-worthy drawing is what we are talking about. And I'm sure you already knew that. You just didn't like that this was referred to as the boreline. I already said call the red line whatever you like. I already knew it wasn't the boreline, technically. But given the context in the discussion it should've been plain as to what I was saying. And I was saying that at 50 m the 1085 fps bullet rises a (corrected) 1" above that red line. Which it does.

uc
 
You must log in or register to reply here.
Back
Top Bottom