What should a tuner be expected to do?

[horseman2]

I'd like to see a tuner test showing a group series shot at the various settings. full in to full out or however it is described
that way the effect on a group size could be seen as it goes toward, through and past the sweet spot

would expect similar results using a Simms LimbSaver Barrel De-Resonator for $20
though the added tuner weight to the forward end may have some complementary benefits to balance

My method of setting the tuner is starting at zero then firing five shots.
Two complete revolutions, and fire five shots followed by two more complete revolution and so on.
By the time I was at 10 revolutions it did not appear the accuracy would be returning anytime soon.
By this time I was looking for something between zero and two revs.
Then I worked in in increments of five clicks and settle some place between 15 and 20 clicks from zero.
It is currently set at 17 and remains there for both 50 yards and 100 metres.
What you requested was kept for some time but as my recall of the specifics faded, it found its way to the shredder.
Somehow it will be about 2500 rounds before that test is repeated but I will keep your request in mind.

 

[Biologist]

If I may summarize, using Toolman's evidence from his post #28:

As I mentioned in my post #11 above, the correct scientific method answer to Grauhanen's original question of "What should a tuner be expected to do?" is, first and foremost, the null hypothesis.

Null hypothesis: Expect nothing. (or re-worded: Tuners have no effect on group size and shape, or precision and accuracy.)

You then try to disprove, or falsify the null hypothesis. You test using methods to control variables, etc, etc. You can falsify it only with repeatable results that show it is not true, i.e. you discovered an effect that is measurable and repeatable.

In Toolman's post #28, and taking him at his word that his data generation has been large enough, Toolman can confidently say: The null hypothesis is now falsified and rejected. The repeatable evidence shows that my tuner does have a measurable effect.

Toolman's new working hypothesis is: My tuner reduces vertical spread by on average 0.118" at 50m/yards (using the example data, as a simple example shown in post #28. I know Toolman's actual data set is large and the stats would be different with the larger data set).

A "working hypothesis" can be converted to a "theory" when the shooting results are repeated enough times that the confidence is very strong. That confidence is achieved statistically when you see the normal distribution bell curve forms. I will take Toolman at his word when he says he has enough replicate data, and so he likely has achieved that normal distribution of results. The new theory is strong for his rifle and ammo.

The Normal Distribution, from Wikipedia, link: https://en.wikipedia.org/wiki/Normal_distribution


Diagram of simple symmetrical Normal Distribution (from free to share, public domain, Creative Commons Attribution. author: M.W. Toews), link:



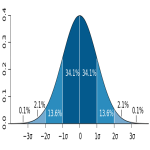
Quote from Wikipedia: "For the normal distribution, the values less than one standard deviation away from the mean account for 68.27% of the set; while two standard deviations from the mean account for 95.45%; and three standard deviations account for 99.73%"

What those SD values are depends on Toolman's larger real life data set.

The shape of the normal distribution and numerical quantity of those SD's on either side of the mean lie at the heart of the OP question for expectations for what the tuner is expected to do.

In Toolman's case, (and I believe him), the expanded answer to the OP question is (using the simple example data): My tuner is expected to reduce vertical on average by 0.118", with one SD of X (where X would be generated from his larger data set).

Note that with the normal distribution, that 2 SD's amount (< 95.45% of the time) means that the hit location for some rounds will be approaching zero difference, for about 5% ish of the time. In a rimfire match standard of 25 round mini bulls, 5% of 25 rounds is 1.25 rounds. That means, on average, about one round in the 25-round match will have very little to no measurable effect by the tuner. However, that is actually quite good odds for using the tuner to win the match.

 

[grauhanen]

I'd like to see a tuner test showing a group series shot at the various settings. full in to full out or however it is described
that way the effect on a group size could be seen as it goes toward, through and past the sweet spot

would expect similar results using a Simms LimbSaver Barrel De-Resonator for $20
though the added tuner weight to the forward end may have some complementary benefits to balance

I'd like to see the kind of testing results you refer to as well. But they don't appear to be easily found. In any case, there is the graph shown below, which is the product of testing at the Eley facilities in the UK, where the rifle was shot from a fixture/vise. It describes the trend between ten shot group size in mm (outside edge-to-outside edge) and the movement of the tuner weight.



The case of the Limbsaver Barrel De-Resonator is somewhat different from that of a tuner. The rubber de-resonator acts more as what's referred to as a "mid-barrel tuner" than as a typical barrel tuner that attaches to the muzzle and has a weight that moves ahead of the muzzle itself. As a piece of rubber it can't be guaranteed to remain where it's placed. Unlike a tuner, it has no reproducible settings that can be checked. Benchrest shooters who shoot with a mid-barrel tuner (usually one made of metal that can be clamped in place by screws) invariably use a barrel tuner at the muzzle as well.

 

[old303]

With a centrefire rifle you tune ammo to your barrel by going up and down tenths of a grain looking for minimum vertical dispersion.

With .22 LR you can't tune your powder charge but you can tune the barrel using a tuner. But it's only .22 LR so the barrel sinewave vibration is a lot less pronounced than with the big loads and the effect is going to be subtle.

 

[Can-down]

With a centrefire rifle you tune ammo to your barrel by going up and down tenths of a grain looking for minimum vertical dispersion.

With .22 LR you can't tune your powder charge but you can tune the barrel using a tuner. But it's only .22 LR so the barrel sinewave vibration is a lot less pronounced than with the big loads and the effect is going to be subtle.

Good point, it would likely take a lot of weight to make a noticeable change on a modern heavy profile short length .22lr barrel shooting target grade ammo at subsonic speeds.

 

[Biologist]

delete.....(I got my wires crossed).

 

[barsik]

I think a rimfire tuner will work if the ammo shows very low SD and ES. barrel time is what makes a rimfire harder to tune.

 

[Leuchtkafer]

I can exemplify by showcasing what happens when a tuner is NOT in the appropriate setting/weight range. The POI of the grouping will shift vertically with a corresponding full rotation of the setting.

https://i.postimg.cc/vZtCqFCq/Tuner-Whip.jpg

When I can rotate the tuner a full turn in either direction and not witness a shift in POI, I consider that to be the appropriate range, the tuner is doing it's job and the hunt for good ammo is now the task.

 

[adamg]

I can exemplify by showcasing what happens when a tuner is NOT in the appropriate setting/weight range. The POI of the grouping will shift vertically with a corresponding full rotation of the setting.

https://i.postimg.cc/vZtCqFCq/Tuner-Whip.jpg

When I can rotate the tuner a full turn in either direction and not witness a shift in POI, I consider that to be the appropriate range, the tuner is doing it's job and the hunt for good ammo is now the task.

I would agree that a significant shift in the point of impact, caused by tuner position, is a strong sign that they do something - and that it could be improving group sizes on this rifle. Personally I never saw this result.

 

[grauhanen]

I can exemplify by showcasing what happens when a tuner is NOT in the appropriate setting/weight range. The POI of the grouping will shift vertically with a corresponding full rotation of the setting.

https://i.postimg.cc/vZtCqFCq/Tuner-Whip.jpg

When I can rotate the tuner a full turn in either direction and not witness a shift in POI, I consider that to be the appropriate range, the tuner is doing it's job and the hunt for good ammo is now the task.

Thanks for offering your information. You say that when a tuner is properly set, the tuner will vertically shift the POI of a group. To be on the same page, you're saying it's the middle group (see below) for which the tuner is doing its job?

At what distance is was the target shot?

 

[Leuchtkafer]

Thanks for offering your information. You say that when a tuner is properly set, the tuner will vertically shift the POI of a group. To be on the same page, you're saying it's the middle group (see below) for which the tuner is doing its job?

At what distance is was the target shot?

**Image and video linking functions will be enabled after you have contributed more to the forum**

No that's the inverse of what I was saying. I'm showing (what I consider) to be the effects of a tuner that is not in the appropriate setting/weight range. I'm having to dig through and find my reference material so bear with me. The testing was done at 50 yards, with a light weight added to the Harrells tuner. I eventually ended up using no weights added to the tuner, here's the full target and one can observe the POI jumping about as I roll through the settings (no notes on how many clicks). I'm not looking at the groups themselves, only that there is POI jump and therefore the appropriate tuner range was NOT found on this target. I'm having some difficulty locating an example where I landed the tuner in the correct range.

https://i.postimg.cc/LsM3GwxC/Light-Tuner-Weight.jpg

Ah, I also see on this that on some settings I only fired two or three shots and moved on if the grouping had a vertical split in it.

 

[grauhanen]

No that's the inverse of what I was saying. I'm showing (what I consider) to be the effects of a tuner that is not in the appropriate setting/weight range. I'm having to dig through and find my reference material so bear with me. The testing was done at 50 yards, with a light weight added to the Harrells tuner. I eventually ended up using no weights added to the tuner, here's the full target and one can observe the POI jumping about as I roll through the settings (no notes on how many clicks). I'm not looking at the groups themselves, only that there is POI jump and therefore the appropriate tuner range was NOT found on this target. I'm having some difficulty locating an example where I landed the tuner in the correct range.

https://i.postimg.cc/LsM3GwxC/Light-Tuner-Weight.jpg

Ah, I also see on this that on some settings I only fired two or three shots and moved on if the grouping had a vertical split in it.

I may still be misunderstanding, but I'll try again. Is the following what you're saying?

Your view is that when the tuner is not properly set the POI will shift vertically or "jump about." In other words, when the POI moves around or jumps, as it does on the target shown, it's evidence that the appropriate tuner setting hasn't been found.

 

[Leuchtkafer]

I may still be misunderstanding, but I'll try again. Is the following what you're saying?

Your view is that when the tuner is not properly set the POI will shift vertically or "jump about." In other words, when the POI moves around or jumps, as it does on the target shown, it's evidence that the appropriate tuner setting hasn't been found.

Yes that is my assessment.

My observation is such that a given barrel requires a certain amount of weight a certain distance ahead of the muzzle to flatline the POI through a given range of settings. If a tuner is too light and does not have enough extension range, this zone will be impossible to reach. Likewise, if a tuner is too heavy, further extension will only exacerbate the vertical dispersion. This is why certain devices such as the Tuna Can have limited success, as I feel it is far too heavy for most barrels. When the tuner weight and range is not appropriate for the barrel, the best one can hope to achieve is analogous to what centerfire reloaders do with respect to tweaking powder charge and seating depth. That is; to time bullet exit at either a high or low peak in barrel flex where there is a momentary dwell before the barrel reverses direction in vertical movement. For us rimfire shooters, we utilize a tuner to modulate the barrel vibration pattern to suit the ammo we are shooting. Given a different ammo or different temperature on a different day, this setting will constantly require adjustment.

With the correct amount of weight the correct distance in front of the muzzle, the vertical movement of the muzzle is nullified (as much as is physically possible). One no longer needs to adjust the setting for different temperature or ammo.

 

[Leuchtkafer]

https://i.postimg.cc/Dy0B5kpq/Node.jpg

The above is to illustrate the mechanics involved, representing a naked barrel. The barrel has a flex node located back from the muzzle, how far back is dependant on the rigidity of the barrel. The stiffer the barrel, the closer to the muzzle the node will be. The "whippier" the barrel, the further back from the muzzle the node will be. As you begin to add weight ahead of the muzzle with a device, this node shifts closer to the muzzle, and the amplitude maximums at the muzzle reduce. When you have enough weight at enough distance ahead of the muzzle, the node is located exactly at the crown, and this is the ideal condition that I seek. If too much weight is added, muzzle amplitude begins to develop again and increase with more weight/distance ahead of the muzzle.

 

[horseman2]

The tuner on my 40XB was originally set for BR50. I do not change it when shooting at 100 metres or yards.
Perhaps some reconsideration is in order but a sweet shooting CZ455 Varmint with the tuner on but after taking it off and back on the accuracy never returned.
Not ready to get bit again.

 

[grauhanen]

Yes that is my assessment.

My observation is such that a given barrel requires a certain amount of weight a certain distance ahead of the muzzle to flatline the POI through a given range of settings. If a tuner is too light and does not have enough extension range, this zone will be impossible to reach. Likewise, if a tuner is too heavy, further extension will only exacerbate the vertical dispersion. This is why certain devices such as the Tuna Can have limited success, as I feel it is far too heavy for most barrels. When the tuner weight and range is not appropriate for the barrel, the best one can hope to achieve is analogous to what centerfire reloaders do with respect to tweaking powder charge and seating depth. That is; to time bullet exit at either a high or low peak in barrel flex where there is a momentary dwell before the barrel reverses direction in vertical movement. For us rimfire shooters, we utilize a tuner to modulate the barrel vibration pattern to suit the ammo we are shooting. Given a different ammo or different temperature on a different day, this setting will constantly require adjustment.

With the correct amount of weight the correct distance in front of the muzzle, the vertical movement of the muzzle is nullified (as much as is physically possible). One no longer needs to adjust the setting for different temperature or ammo.

https://i.postimg.cc/Dy0B5kpq/Node.jpg

The above is to illustrate the mechanics involved, representing a naked barrel. The barrel has a flex node located back from the muzzle, how far back is dependant on the rigidity of the barrel. The stiffer the barrel, the closer to the muzzle the node will be. The "whippier" the barrel, the further back from the muzzle the node will be. As you begin to add weight ahead of the muzzle with a device, this node shifts closer to the muzzle, and the amplitude maximums at the muzzle reduce. When you have enough weight at enough distance ahead of the muzzle, the node is located exactly at the crown, and this is the ideal condition that I seek. If too much weight is added, muzzle amplitude begins to develop again and increase with more weight/distance ahead of the muzzle.

You demonstrate as good an appreciation of tuner function as has appeared recently on the Rimfire forum.

There is a debate among rimfire shooters as to how the rimfire tuner does its job. Among the earliest explanations to gain traction and popularity are two that still seem to dominate the discussion. One is that tuners work by achieving positive compensation by means of timing bullet exit from a muzzle that is moving. In brief, slower bullets exit on a higher upward muzzle movement than faster ones. If correct, this explanation requires tuner adjustment for changes in distance to target.

Another early explanation was that a good tuner setting caused the node to be at the muzzle so that it was not moving, "stopped" as it were.

Unfortunately, there seems to be no agreement. What's clear, however, is that it can't be both at the same time.

Experienced and very serious rimfire BR shooters still differ on whether different lots of ammo or different conditions such as temperature require tuner adjustment. I suspect the balance would tilt in favour of the "set and forget" position, that once correctly tuned it works for all good ammo. After all, they would say, it's the barrel that is being tuned, not the ammo.

In any case, it's worth noting that it was curious that the explanation offered above in posts #48 and #51 were based on the ostensible absence of evidence that a tuner was working, which is to say the target was supposed to show when a tuner wasn't doing its job.

Without knowing more details, it remains possible that the target didn't show that the tuner was or wasn't doing its job simply because the ammo didn't do its job. In other words, if the ammo isn't consistent it can be very hard to know what, if anything, a tuner might be doing.

 

[Williwaw]

I tell myself that I should know better than engaging another tuner thread but I find the topic so compelling I can't help myself.

To answer your original question ... a tuner can be expected to reduce the vertical dispersion of the POI attributable to velocity variations.

If correct, this explanation requires tuner adjustment for changes in distance to target. I think the ability of a tuner to achieve full PC is maxed out somewhere between 50 and 100 yards so you are correct in theory but maybe not in practice.

"set and forget" Probably works some of the time because the velocity characteristics of the different lots are sufficiently similar that the differences are not revealed given the equipment, the environmentals and the shooter himself. This is consistent with the fact that some of the set and forget it crowd go to the test centers with their tuners on.

 

[wallz]

Me personally, I have a tuner that I use. It is mounted on an 18" heavy barrel, beit a stock barrel on an annie 1727.

The particular lots that I have of midas+, center X and sk long range were all printing pretty nice groups at 50m. I mean less than .5". As soon as I extended the range out to 100m those same groups all went to snot. Printing over 1.5". Same ammo, same lots, same rifle, same shooter, same bags, same day, same or close to same conditions, just at 100m distance. Stock configuration, no tuner used or mounted.

That is were I mounted the tuner and started to play with it at 100M. I have been able to get those groups down much smaller and tighter after tuner work. Best goups with center X were printing at .550", midal+ @ .661". They were at a different tuner setting to get those smaller groups for the different ammo types used. Just now thinking, that I never did try 50m with the tuner on printing the small groups at 100m, but will on the next range trip if I get a chance.

Now this is with the factory stock, and I have a new custom stock in the works that will take care of the short comings of the factory wood stock on the 1727. I really wanted to wait for the new stock before I started to play with the tuner, but I am impatient. I have word that it is finally on its way to Canada, so will be sending my action in for custom fitting into the new stock, then can really start to see some results with a solid stock as a good base to shoot from.

My understanding has always been the "barrel harmonics" and "whip" is created with the charge going off in the chamber and bullet exit through the barrel. Pressure created with charge going off. Yes the tuner weight, barrel length, chamber cut, barrel type all will have a play in this as well. I see this with my center fire rifles as well. When I increase the powder charge, keeping everything else the same, I will get impact shift points. And I'm talking 26" heavy stainless barrels with an added brake/tuner on the end. I use a tuner on this barrel as well, and see the same kind of impact shifting when I use the tuner to adjust the load that I use. You get to see this a little more in the center fire, because you get a bit more consistency with the ammo, and see impact shifting with the different tuner settings. I set it up at 100m, and then see no real shifting after that out to distance, even as the barrel heats up. Yes there is some heat shift, but I tune it during the heating process in 20 or more shooting strings, so that is factored in somewhat.

Does the inconsistent ammo play with the impacts down range, yep. You get to see it in the groupings on the 22 compared to the center fire.

 

[grauhanen]

I tell myself that I should know better than engaging another tuner thread but I find the topic so compelling I can't help myself.

To answer your original question ... a tuner can be expected to reduce the vertical dispersion of the POI attributable to velocity variations.

If correct, this explanation requires tuner adjustment for changes in distance to target. I think the ability of a tuner to achieve full PC is maxed out somewhere between 50 and 100 yards so you are correct in theory but maybe not in practice.

"set and forget" Probably works some of the time because the velocity characteristics of the different lots are sufficiently similar that the differences are not revealed given the equipment, the environmentals and the shooter himself. This is consistent with the fact that some of the set and forget it crowd go to the test centers with their tuners on.

It's good to see you responding here on CGN. Your experience and insight is helpful, especially to readers who may not peruse many other rimfire forums and discussions.

The "set and forget" side includes serious BR shooters who insist that once their tuner is correctly set, they haven't had to touch it in years, regardless whether they go to test centers. Some of them no doubt self test as they have for years, others may go to test centers. Nevertheless, reliance on test centers can indeed foster the fallacy that they can supplant a more comprehensive understanding of riflle and ammo (and tuner). As you know from your own shooting, there's no substitute for as much first hand experience as possible.

In any case, if they are not wrong about set and forget, it may be testimony to the relationship between tuners and good ammo. While many lots of good ammo often have overlap in ES ranges, if PC explains tuner function, tuners may well work just the same no matter the ES range. They just need good ammo to do what they can.

 

[Toolman]

The set and forget hasn’t worked for me for whatever reason.

I know my setup very well and it’s easy for me to see when it’s not humming along.

Last match I shot at two weeks ago I started out on a known good tune but I was seeing more vertical than usual, so I clicked out two clicks……..a little better but still lacking. Another couple of clicks and boom……gun flattened out and all was good from there.

I don’t completely understand the mechanics of why but it’s my first hand experience.