here is 1 of 4 tools i useand jerry being really stupid again as we dont use #### ammo for benchrest
Jerry go to the doctor and get better pills as you seem to need them
Resizing, rim / weight sorting
- Thread starter GPSMapNut
- Start date
here is 1 of 4 tools i useand jerry being really stupid again as we dont use #### ammo for benchrest
Jerry go to the doctor and get better pills as you seem to need them
some of my dozen REAL RIMFIRE BENCHGUNS
plus between 3 of us we have about quarter of a million rimfire be chrest rounds of 22 long rifle, none of which is low enough to use in jerrys savage rifles
not pictured are 2 VUDOO single shot rifles in 2 macmillan and a ROTEX stock
also 3 jerry stiller built rifles in rotex stocks
over 100 grand in rimfire rifles and ammo with 2 seb neo-x rests and 2 one oiece rests for competition and testing along with 2 rail guns
Jerry is not very bright when it comes to REAL BENCHREST STUFF
the guy named shorty on here is way smarter than i will ever be and folks should listen to what he and his close friends say
put jerry on ignore for rimfire benchrest he knows virtually nothing to add here
Not tearing him down just stating facts
the fellow friend I chum around with has travelled the world for 3 p shooting and world cups for canada
one of his coaches is in Australia or new Zealand forget which country
he used to,shoot over 25 thousand rounds a year to be competitive
some of us are REAL SERIOUS about this stuff and every so often try to help others
I used to spend a few hours on the phone weekly helping new shooters discover rimfire benchrest
now I mostly charge for that privilege and find I have more time to spend with folks who appreciate the knowledge and will actually listen and try the advice
plus between 3 of us we have about quarter of a million rimfire be chrest rounds of 22 long rifle, none of which is low enough to use in jerrys savage rifles
not pictured are 2 VUDOO single shot rifles in 2 macmillan and a ROTEX stock
also 3 jerry stiller built rifles in rotex stocks
over 100 grand in rimfire rifles and ammo with 2 seb neo-x rests and 2 one oiece rests for competition and testing along with 2 rail guns
Jerry is not very bright when it comes to REAL BENCHREST STUFF
the guy named shorty on here is way smarter than i will ever be and folks should listen to what he and his close friends say
put jerry on ignore for rimfire benchrest he knows virtually nothing to add here
Not tearing him down just stating facts
the fellow friend I chum around with has travelled the world for 3 p shooting and world cups for canada
one of his coaches is in Australia or new Zealand forget which country
he used to,shoot over 25 thousand rounds a year to be competitive
some of us are REAL SERIOUS about this stuff and every so often try to help others
I used to spend a few hours on the phone weekly helping new shooters discover rimfire benchrest
now I mostly charge for that privilege and find I have more time to spend with folks who appreciate the knowledge and will actually listen and try the advice
Attachments
Indeed. He has single-handedly helped explain, among other things, why .22LR group size can be smaller further out than closer (e.g. a lot that shoots best at 100 will shoot worse at 50), why barrels are best at certain specific distances and not at any other, and why lots that shoot best at 50 can't shoot best at 100. We need more of this.
Your inability to understand math does not change math. *pat pat*
I love that fuzzy Xmas spirit spurting warm froth line…and I think I know why It’s happening and why It’s good.
Dedicated shooters try harder. Precision shooter go into rabbit holes with gusto AND shovels. Once in a rabbit hole one’s view of the ‘world’ is limited and obscured to other adjacent rabbit holes.
99% of men that shoot have BIG testicles and therefore are ‘gifted or encumbered’ with a level of stubbornness that validates their opinion. Sorry girls and transgenders… lol
The positive aspects of considering other less qualified opinion givers is this…the other person may still be right OR WRONG… that is a discovery in itself!!!! We may go scouting into a forest looking for signs of scapes and rubs and instead find an abandoned stolen car or a pot plantation. Keep your eyes and mind OPEN and above all use some common sense, take things with a grain of salt, and have a sense of humour and wear a smile on your face. Right ?? lol ….cheers !!
Math don't shoot.
Don't know if you do any longer, either. Seriously, Shorty, as an example you have insisted convergence with .22LR regularly happens (when groups are smaller in MOA further out than closer in). You have no reliable evidence to support this bizarre view, not even math.
When Bryan Litz, a widely respected ballistician, says convergence doesn't occur (except by accident) you've declared that he's wrong without explanation. That's not sound, it's not even math.
Promoting wrong-headed ideas is unfortunate and it's made worse when some readers of this forum may naively believe you.
Jingle Bells, everyone.
You not being able to follow along with explanations doesn't mean no explanations were given. Math is math. Physics is physics. And I've shown you the work many times over. Your (in)ability to understand it doesn't change any of it. Not even having the name Bryan Litz will change physics. (He also says tuners don't work. So why do you have tuners, Glenn? They work on the principle of convergence. Tuning/positive compensation is making convergence happen where you want it to happen. If convergence isn't a thing, and tuners don't work, then I guess you should've removed them from your rifles long ago, right? Are you going to be removing them now? Heh.)Math don't shoot.
Seriously, Shorty, as an example you have insisted convergence with .22LR regularly happens (when groups are smaller in MOA further out than closer in). You have no reliable evidence to support this bizarre view, not even math.
When Bryan Litz, a widely respected ballistician, says convergence doesn't occur (except by accident) you've declared that he's wrong without explanation. That's not sound, it's not even math.
Promoting wrong-headed ideas is unfortunate and it's made worse when some readers of this forum may naively believe you.
Jingle Bells, everyone.
This is an example of how a barrel vibrates during the firing cycle. It shows time since ignition on X, and change in launch angle on Y. It will do this in the same manner every single time you fire a shot. How "exciting" the ammo is will change the magnitude in the Y direction by imparting more or less energy. It has no effect on the X direction. Just like how hard you strike a tuning fork will change how loud it is, not the frequency you hear. Gently tap an "A" tuning fork and you'll hear a very quiet 440 Hz, and if you give it a really hard whack you'll hear a much louder 440 Hz. A given ammo will have a given average exit time, a window of a given width during which all shots will exit. This determines the window of launch angle of those shots. And the launch angle combined with the muzzle velocity will play important roles in where those shots land on your target, as does how far away you have placed your target. You determine the gross launch angle by dialling in your scope, and the combination of the barrel's vibrations and bullet exit timing determine the fine launch angle alteration. The exit window (and bullet shape consistency, and environmental effects if you wish to include those) determine the variance at the target.
When you test different brands/models/lots of ammo, you are finding lots that fall more favourably along the curve. A lot number that has more shots exiting from 2.1-2.2 ms in this example will give you better results than a lot number that has more shots exiting from 1.90-2.0 ms. Why that is should be apparent from looking at those regions of the line graph, providing you have a somewhat decent grasp of basic ballistics theory, most especially if you understand positive compensation. You don't want any shots to leave during downswings, ever. Downswings increase elevation variance at the target.
What's that got to do with sorting by rim thickness? Sorting by rim thickness reduces variance in ignition timing. A reduction in variance of exiting timing logically follows. Sorting by rim thickness could shrink the exit timing window from, say, a 0.25 ms region to a 0.2 ms region, as an arbitrary example. That means more shots behaving in a more similar manner. The wider that window is, the more chance there is of different things happening. But I suspect ammo manufacturers have long been taking care of this particular aspect for us be providing us with more consistent brass.
Shorty, after previous efforts to get you to explain met with your refusal to respond, I glad you have given your best answer. Unfortunately it remains unsatisfactory, graph notwithstanding.
The following are your own words from a previous post on this forum.
Many shooters make the erroneous assumption that dispersion increases with distance, that group size only becomes larger as distance grows. This is incorrect.
Beginning from the muzzle, dispersion increases until about halfway to the ideal distance at which convergence occurs. From about the halfway point up to the ideal distance group dispersion begins decreasing again in terms of MOA.
Your idea is that a good rifle will shoot to a larger MOA at about 25 or so yards than at 50 (or at 50 than at 100). That's nonsense. It's doubtful anyone, including you, will find evidence from elsewhere that supports your view.
Gravity and MV variation alone ensures that dispersion is less at 25 than at 50 or less at 50 than at 100. It might help your position if positive compensation was perfect and completely achieved. Of course, it's not.
Nothing further need be said unless someone wishes to support Shorty with reliable information.
.
The following are your own words from a previous post on this forum.
Many shooters make the erroneous assumption that dispersion increases with distance, that group size only becomes larger as distance grows. This is incorrect.
Beginning from the muzzle, dispersion increases until about halfway to the ideal distance at which convergence occurs. From about the halfway point up to the ideal distance group dispersion begins decreasing again in terms of MOA.
Your idea is that a good rifle will shoot to a larger MOA at about 25 or so yards than at 50 (or at 50 than at 100). That's nonsense. It's doubtful anyone, including you, will find evidence from elsewhere that supports your view.
Gravity and MV variation alone ensures that dispersion is less at 25 than at 50 or less at 50 than at 100. It might help your position if positive compensation was perfect and completely achieved. Of course, it's not.
Nothing further need be said unless someone wishes to support Shorty with reliable information.
.
That may be the best example of a hijacked thread that I've ever seen.
Without hard data I can only comment as a mathematician and physicist and a guy having a ####load of practical mechanical engineering...
Shoty's divination regarding barrel harmonics make perfect sense. 1 up for tuners. Convengergence make sense but... at hardly predictable distance so it's a wash.
Sorting by ... whatever parameters you choose make sense if only to eliminate something factory missed... Sure, statistically, it may be pointless when dealing with $20 a box ammo but viable for $3 a box...In other words, you are all right and wr6at the same time...In yet another words; there is no frigging way that culling rounds that vary more than 10% in weight and matching rim thickness to gun headspace and bullet diameter to the barrel ( all that in no particular order) would not have impac8on the group size...
Glenn, it is basic ballistic theory. Go here:
https://www.jbmballistics.com/cgi-bin/jbmtraj-5.1.cgi
Select Eley Club for the bullet. That will make it use the appropriate values for the first three entry boxes, so what they say will then be irrelevant. Here are the rest of the values used, most of which should just be default already, and some that are irrelevant but listed anyway:
Muzzle Velocity: 1060
Distance to Chronograph: 0
Sight Height: 1.5
Sight Offset: 0
Zero Height: 0
Zero Offset: 0
Windage: 0
Elevation: 0
Line Of Sight Angle: 0
Cant Angle: 0
Wind Speed: 0
Wing Angle: 90
Target Speed: 0
Target Angle: 90
Target Height: 10
Minimum Range: 0
Maximum Range: 100
Range Increment: 1
Zero Range: 50
Temperature: 59
Pressure: 29.92
Humidity: 0
Altitude: 0
Vital Zone Radius: 5
Energy Column Formula: Energy (ft-lbs)
Column 1 Units: 0.1 in (to move the decimal place one spot to get another decimal of accuracy to be output)
Column 2 Units: 0.1 MOA (same accuracy deal)
Elevation Correction for Zero Range: checkmark
Windage Correction for Zero Range: no checkmark
Range in Meters: no checkmark
Target Relative Drops: checkmark
Zero at Max. Point Blank Range: no checkmark
Mark Sound Barrier Crossing: no checkmark
Include Extra Rows: no checkmark
Round Output to Whole Numbers: no checkmark
Include Danger Space: no checkmark
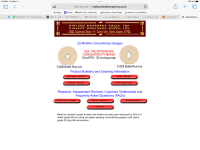
After hitting Calculate with all of that set and recording the results I then hit Back in the browser to get back to the input page, and I change the muzzle velocity from 1060 to 1085 and hit Calculate again and record that data. That gives this after dividing the drop by 10 to bring us back to the proper decimal places and gives this, which you can double check for yourself by entering the same stuff into the same calculator:
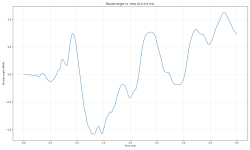
And results in this graph of drop versus yardage for both shots:
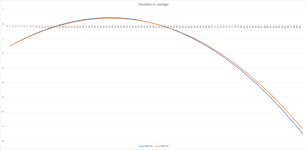
That gives you two shots, one at 1060 fps and one at 1085 fps, from a rifle that has been tuned for 50 yards. As you can see in the data, the elevation delta starts at 0 at the muzzle and grows until about the halfway point to the target, and the dispersion maxes out at 0.05" at the 28-yard mark. After that point it continues falling until it reaches the 50-yard target and tuning point, at which point the delta is 0, or going through the same hole. After that point the dispersion continues growing until the end of our data at 100 yards. It would continue growing past that point if you care to enlarge the data pool. If you change the tuning point / target distance / zero distance to 100 yards instead and calculate the data out to 200 yards you will see a similar thing happen, only with the dispersion steadily growing until somewhere around the 40-60 yard region, the exact answer being limited by the decimal places that this particular calculator is capable of, and then shrinking until we get to the 100-yard tuned/target distance. And, again, after that point it will begin growing again and will continue growing. That's just basic ballistics. If you can tune for a particular distance that's what will happen. If you don't tune at all and just live with what the barrel naturally does then you could figure out what the barrel's natural tuning distance is with a given ammo by shooting lots of shots at a lot of distances. And once you figure out what that natural tuning distance is you will see the same pattern, where the dispersion steadily grows from the muzzle until about halfway to that natural tuning distance and then it will decrease until it reaches that distance. And beyond that distance it will continue growing as you go further and further out.
Every single barrel that has ever shot a projectile behaves in this fashion. The only barrel that would not exhibit this behaviour is one that is incapable of flexing. If you had a "barrel" made out of a solid 1-cubic-metre block of steel that had a 22 LR bore drilled, reamed, rifled, lapped, chambered, and crowned through the centre of it and attached an action to it then it probably would not flex enough to notice any flex at all. And you'd get dispersion exactly equal to the amount of muzzle velocity variation seen present in the ammo. It would start at 0 at the muzzle and continually grow from that point forward, exactly as you describe and imagine it does with the actual barrels you own. But the problem is none of the barrels you actually own are devoid of flex. They all flex. Every single one of them. They all flex during firing and the vibration pattern that is present because they can flex makes them behave exactly as I describe, not as you imagine. Your supposition is only correct in the example of a barrel that is incapable of flexing and thus vibrating. Since all of our barrels flex and vibrate your supposition is incorrect. They all have their own unique vibration pattern, as the one I showed earlier would be unique to the barrel it is patterned on. This is what determines how they behave with any given ammo at any given distance. This is what gives them their own unique natural tuned distance. And it is what allows one to use an add-on tuner to alter that tuned distance, hopefully in a favourable manner for your target distance of choice.
It isn't *my* idea. It is basic ballistic theory that anyone can confirm with their own ballistic calculator of choice. It's basic physics. It's just math. It's the physical world doing what it does due to the rules it follows. It's got nothing to do with me or what I think. Like I told you before, Glenn, take one of your shooting days and set it aside to do a test where you'll fire 100 shots at 10 yards, 100 shots at 20 yards, 100 shots at 30 yards, 100 shots at 40 yards... on up to 100 shots at 100 yards without touching any of the controls on your rifle other than the parallax to ensure you're focused to see the target and check out the results for yourself. You might find the current tuned distance within that first 100 yards, or you might have to continue the experiment beyond that to find it, but that tuned distance is there to find. The smallest amount of dispersion in terms of MOA will not be as close as you can get to the gun, bar not being able to actually measure small enough at that distance. Using OnTarget's practice ARA target #7 and shooting one shot per bull will help get around that issue by allowing you to scan them and place the shots pretty accurately in the program, allowing it to give you pretty accurate measurements. You'll find something similar to this ballistic calculator exercise. The distances that the various things happen at will be up to your barrel's behaviour, but you will find the same things. Dispersion growing until around the halfway point of the tuned distance, shrinking until it reaches that tuned distance, and then continually growing once beyond that. That's just ballistics.
Last edited:
From the very beginning in the Garden, mankind has sought knowledge and understanding of everything, including those things that are beyond explanations. We shooters are bad for this, figuring that there is an explanation when we despite our efforts, we see results that unexpectedly deviate outside our expectations or desires, despite our best efforts. Precision shooters and engineers share the same trait... they both see everything as a problem to be solved. Many can be, but not all.
Numbers, graphs and charts can be compiled from data to support almost any theory, but a theory remains just that, theoretical.
There are lots of shooting stuff that is explained by science and math, there are also lots of things that leave us scratching our heads. This won't stop me from striving to do better or make me abandon the hunt for the perfect ammo.
Numbers, graphs and charts can be compiled from data to support almost any theory, but a theory remains just that, theoretical.
There are lots of shooting stuff that is explained by science and math, there are also lots of things that leave us scratching our heads. This won't stop me from striving to do better or make me abandon the hunt for the perfect ammo.
This is an excellent point.
Yogi Berra, baseball catcher and manager, put it this way -- In theory there is no difference between theory and practice. In practice there is.
Further comment on the question of convergence can be made here https://www.canadiangunnutz.com/forum/threads/group-convergence-with-22lr-yea-or-nay.2551723/
Leuchtkafer
Member
Within the parameters that the headspace isn't so tight that it is crushing rims, or so loose as to negatively impact ignition consistency (firing pin over-travel stop), you'll be hard pressed to detect an accuracy difference.
